Difference-in-differences (DiD) estimation is a type of quasi-experimental impact evaluation method that permits to control time-constant differences in unobservable variables. The method admits that differences between control and treatment groups can exist (such as different averages in socio-economic status for instance). By combining before-after and simple difference analysis, DiD addresses shortcomings of both approaches such as maturation bias or selection bias that result from time-constant unobservable variables.

However, a main disadvantage of DiD compared to controlled designs such as RCTs it is reliance on a common trend assumption. This assumption presupposes that, in the absence of intervention, treatment units and comparison units would have experienced the same evolution over time. The common trend assumption is subjected to many threats and can easily be violated. In fact, even in the case where the two groups may look similar at baseline, at least on observable variables, nothing guarantees they will follow similar trends, as some confounding factors may intervene. For example, if the DiD is designed based on geographically non-overlapping control and treatment groups, this entails the risk that some unforeseen events affect only one of both groups. In the course of the implementation of an educational program for instance, schools of the treatment group might be affected positively by other governmental education programs resulting in a bias in the impact estimates. Similarly, the occurrence of a natural catastrophe such as flooding or an earthquake may cause treatment schools to close for several months, thus impacting negatively on school outcomes. To sum up, unless schools are chosen in a randomized manner like in an RCT design, the existence of some unobservable factor that unequally affects both groups over time can hardly be excluded. It is therefore hard to validate the common trend assumption upon which DiD relies unless multiple time periods are available.

Linear regression models usually utilized so far were based on the implicit assumption that all individuals are affected by an intervention in the same way. This assumption is often implausible, though. Rather, one would expect that some people are affected more than others by a policy change or a particular program. Some people may benefit a lot while others to a much lesser extent. The effects might differ by quantiles and be context dependent. It is thus important to ascertain who and how many people lose or gain from a certain reform alternative. This means that not only average gains or losses need to be assessed but also the distribution of the effects should be analyzed, especially in fields where inequality of opportunities or outcomes particularly matter, e.g. education, health, incomes and poverty. New econometric methods based on nonparametric models admit analysis of heterogeneity and distributional effects, thus allowing a much more differentiated approach to impact evaluation.

Impact evaluations with heterogeneity analysis specifically account for the inter-individual and inter-group diversity and for differences in the impacts that certain interventions may have. Such heterogeneity in effects needs to be analyzed in order to learn which intervention or program works best for whom. Impact heterogeneity analysis, if embedded in the analysis of controlled trials as well as quasi-experimental designs, presents interesting potential to find and develop tailored optimal solutions.

To provide a concrete example of effect heterogeneity, one can imagine that supplying new, pedagogically adapted textbooks would improve especially the learning outcomes of students who used to perform lower previously. It may be that the program has an average treatment effect of zero, but does have a positive impact on lower-achieving students. In the context of granting chance equality through education, adoption and scaling-up of the program may make sense, even if average impacts are small. Such effects on inequality would be missed by conventional regression models. The ability of quantile treatment effects to characterize the heterogeneous impact on different points of an outcome distribution makes them appealing in many applications.

In a phase-in design, the development program is implemented in stages. In the first years a limited number of households, villages, schools or health posts benefit from the program, with subsequent coverage increasing in the following years. This is a natural approach in the implementation of many development programs. A phase-in design presents the advantage that the control group is excluded from the program only temporarily. Delaying program roll-out in the control group even for just a short period of time (e.g. 2-3 years) is still very useful for allowing the implementation of an RCT and therewith drawing solid conclusions about the program’s impacts. A rotation design offers to switch program implementation between groups. For instance, in year 1, groups that were randomly selected as participants will receive the program, while control groups do not. In year 2, the program is implemented in the former control groups and no longer in the first group. For this design to produce unbiased estimates, however, absence of interaction between the cohorts is required.

A Portfolio Evaluation most of the time uses mixed methods to generate a description of the overall portfolio under study. Since a counterfactual analysis is not possible for evaluating the portfolio, most evaluations will use primarily qualitative methods. Qualitative methods can provide rich contextual information that provide insight into how and why interventions create impact.

Propensity score matching (PSM) is a quasi-experimental econometric method where program recipients are matched to non-participants based on observable characteristics. The difference in outcomes between matched observations is then attributed to the program.

Randomized control trials (RCTs) represent the most reliable evaluation designs in social sciences, where laboratory experimental designs as in the natural sciences are not applicable. Akin to medical experiments, control trials ensure that control groups are really comparable and that we are comparing “like with like” when estimating impacts.

RCTs are based on two main components:

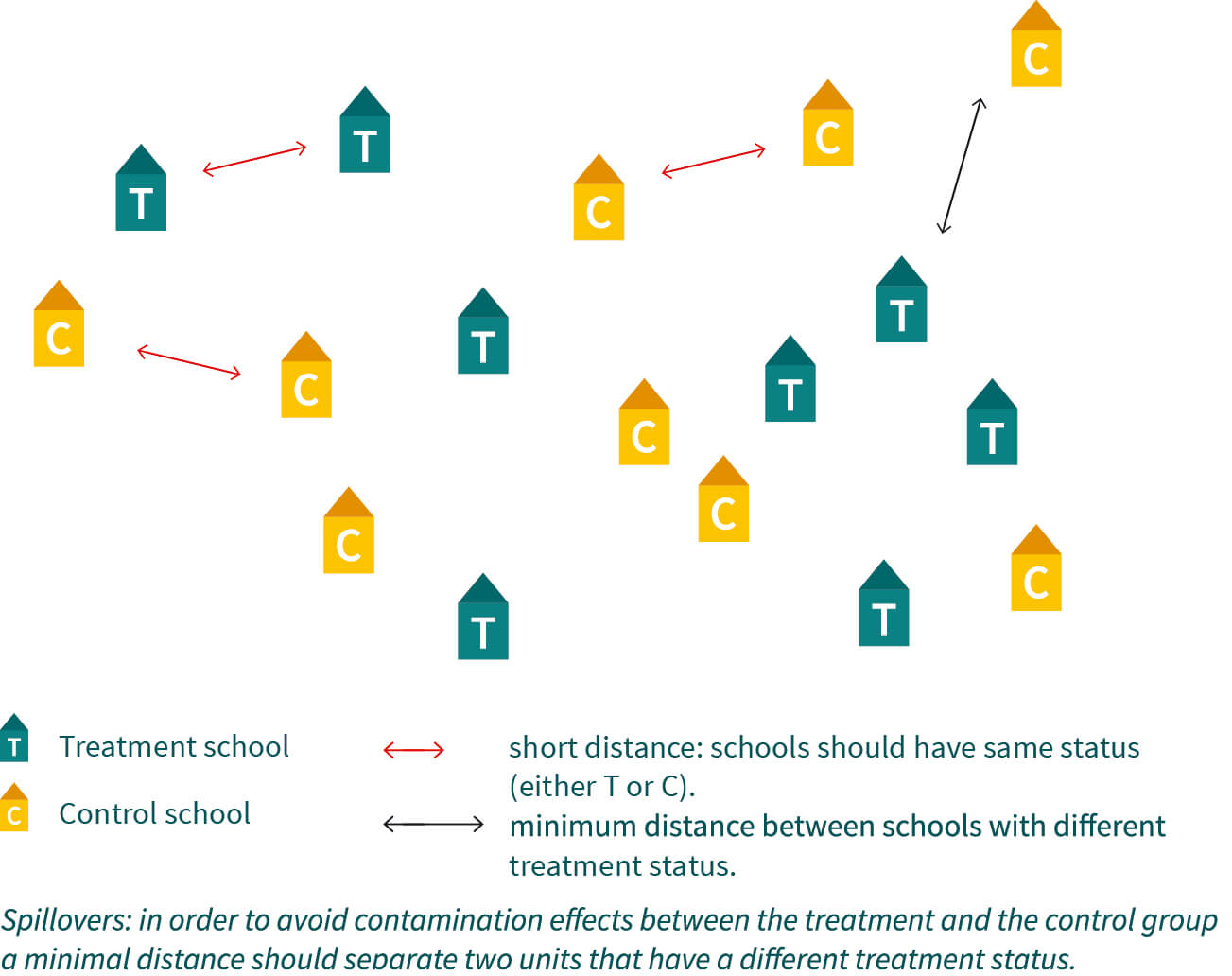
• Control group: There is a control group, used to construct the counterfactual outcome. The control group is not supposed to be covered by the program (the intervention, or treatment) nor should it by affected by spillovers (the fact that others are receiving the program).

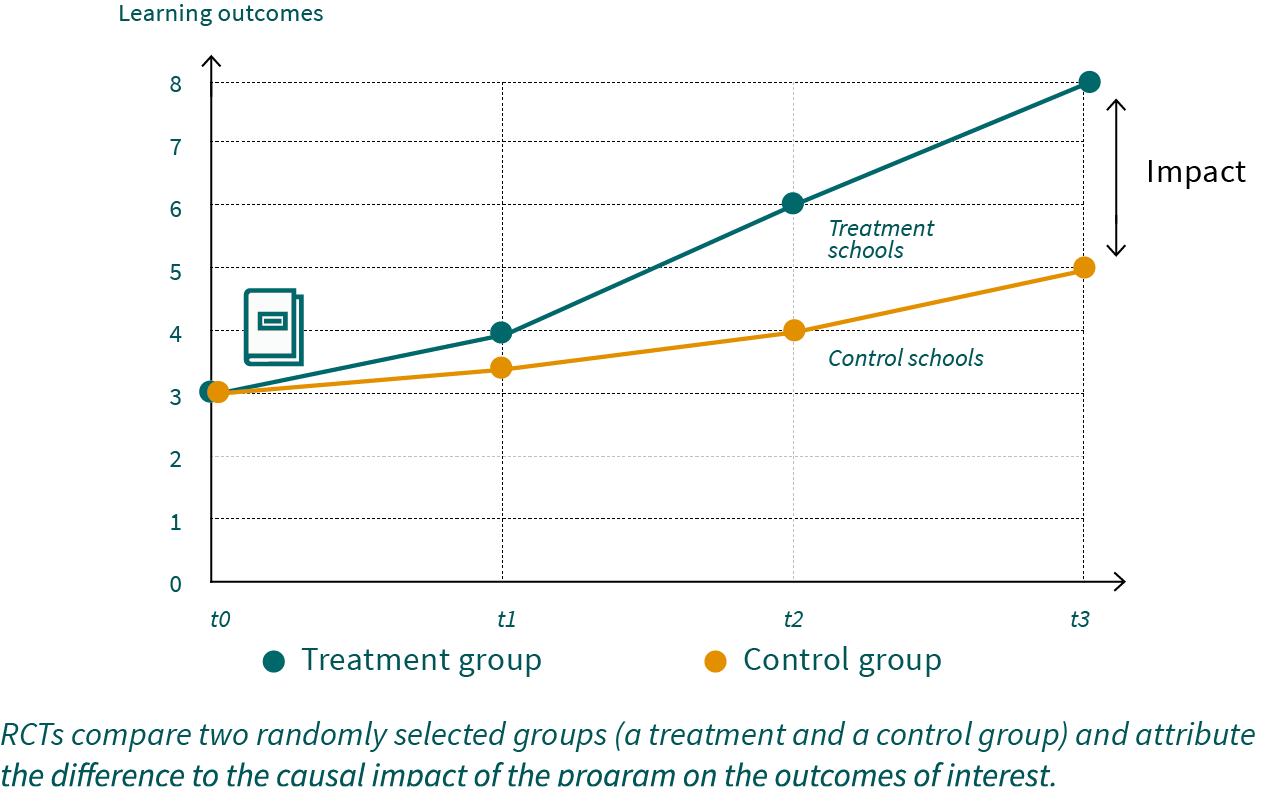
• Randomized trial: Potential beneficiaries are randomly allocated either to the treatment group or control group. This ensures the equivalence, that is, the comparability of the groups on all observable and unobservable characteristics at baseline. If sample sizes are sufficiently large, randomization eliminates all confounding factors and selection bias, as both groups will differ only with regard to their treatment status. The outcomes of the program can therefore be compared on ceteris paribus conditions (other factors being equal).

RCTs therefore allow causal attribution, since observed differences in outcome variables can be attributed to the program itself. In other words, the observed difference between the program and the control groups represents the impact that has been generated because of the program. The randomization process furthermore ensures that impact estimates will be consistent without any assumptions. This is a major advantage as compared to observational quasi-experimental methods, which often rely on untestable ad-hoc assumptions. Therefore, control trials represent the most rigorous, unbiased method to measure impacts and establish causal effects and pathways.

Many development interventions are implemented at cluster level through schools, health posts, microfinance branches, village and community organizations, for instance. In such cases there may be compelling reasons to allocate all individuals or households that belong to the same cluster to the same kind of intervention status (treatment or control). For instance, all children of a given school should be allowed to participate in an educational intervention. Similarly, all households served by a given health post should benefit from an extended health program. In such situations, the random assignment of treatment versus control needs to be based on the level of the school or health posts (the cluster), instead of the individual or household. This prevents unfairness within clusters as well as the occurrence of spillovers. This method is referred to as cluster randomized control trials (C-RCTs). Whereas C-RCTs are conceptually like RCTs, they have relevant design implications, particularly with respect to sample size.

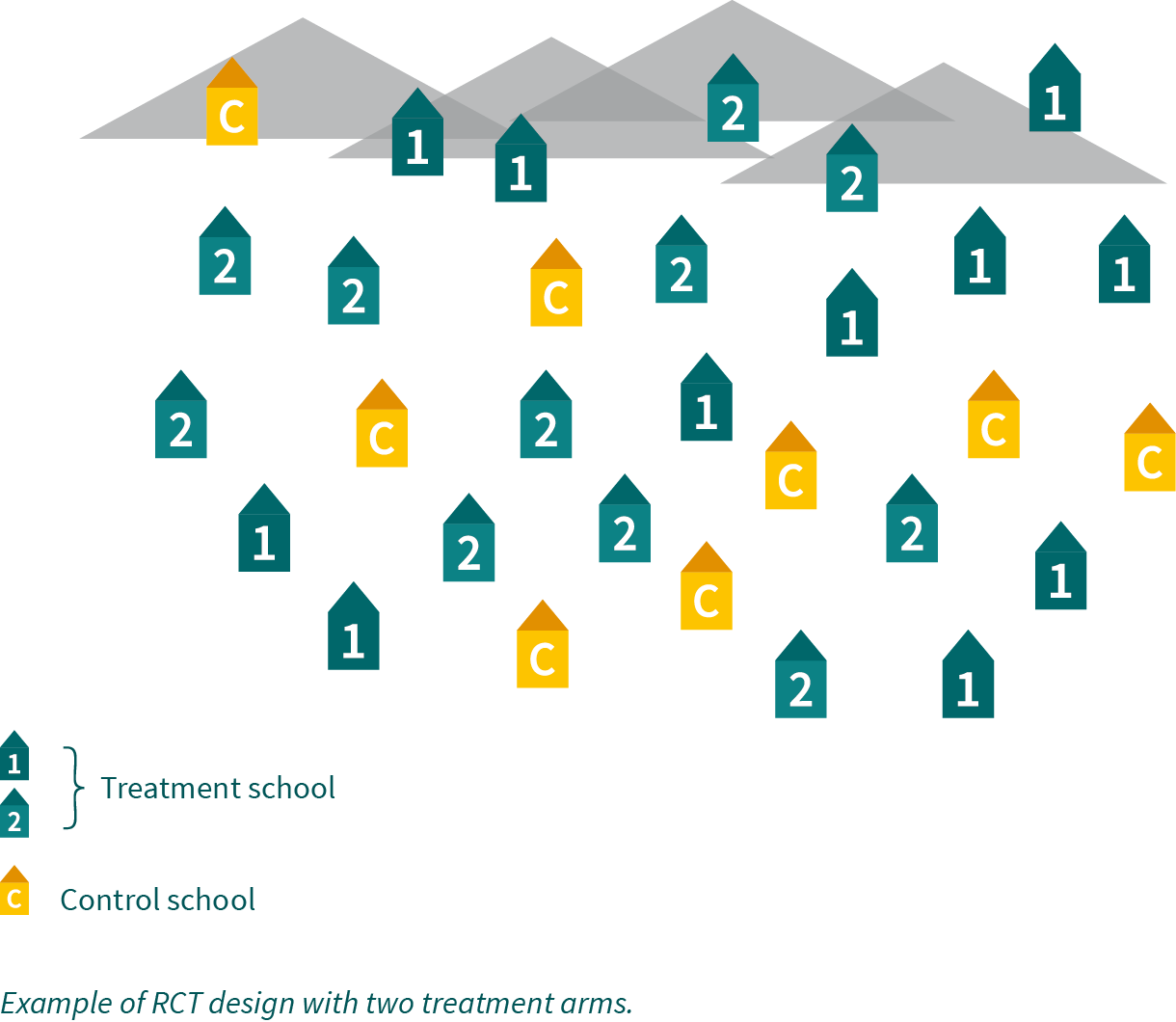
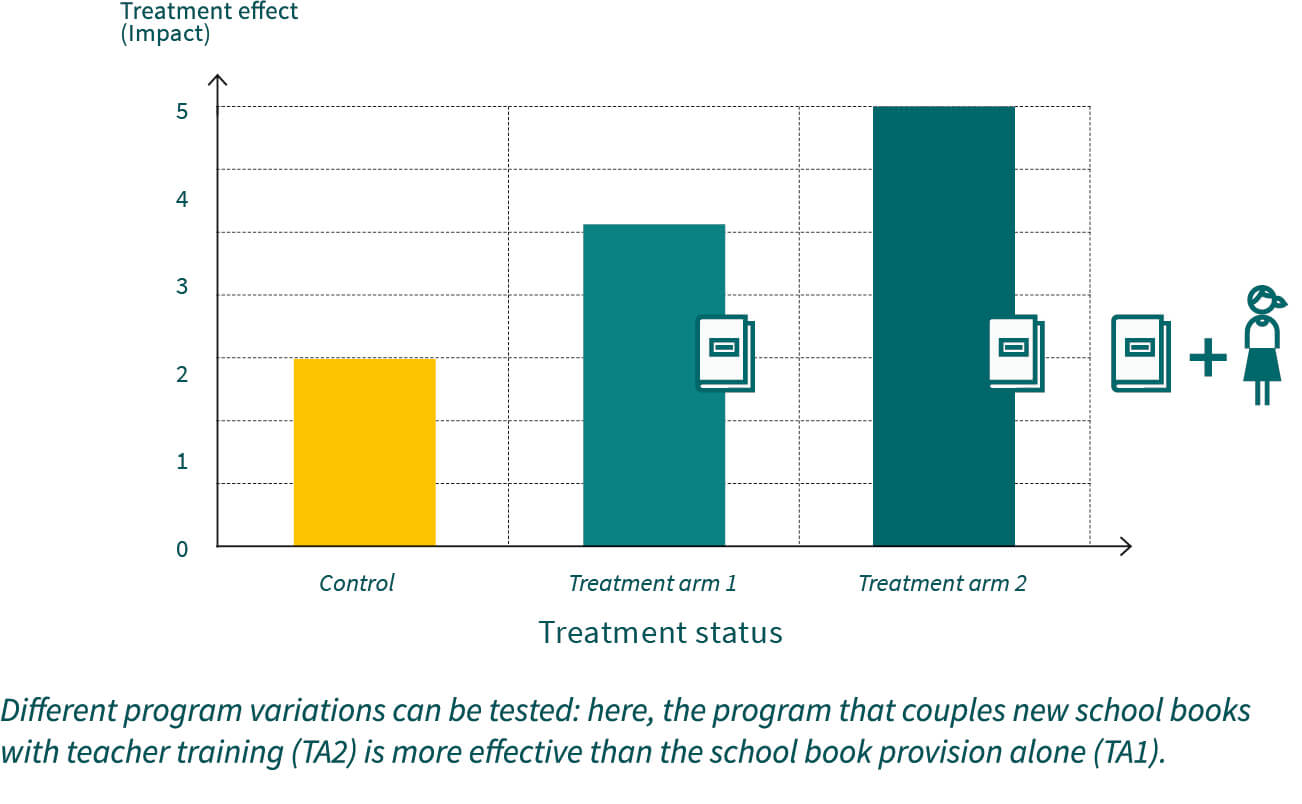
Impact evaluation is not only about assessing whether a program worked or did not but shall also produce insights and recommendations for improving it. One would need to know, for example, whether the program’s impact can be improved by way of combining or augmenting it with other interventions. Analyzing the extent to which impacts depend on contextual and implementation factors can be attempted via regression methods. While this can provide suggestive evidence such approaches are exposed to risks of selection bias. In contrast, controlled trials with several program variations, also referred to as treatment arms, represent the ideal approach for learning about how to improve development programs. For example, in an educational program in which new schoolbooks are supplied, one would like to know whether additional teacher pedagogical training is requisite or whether the books alone are sufficient inputs. In such setting, schools in the first

treatment arm (TA1) would only receive books, while schools in the second treatment arm (TA2) would receive books and additional teacher pedagogical training in combination. In addition, a control group remains for estimating the impacts of books and training as compared to the absence of any intervention – the control group could even be dropped, if one were only interested in the differential impact of the additional training. In any case, the allocation of schools to treatment arms must be based on a randomization protocol in order to avoid selection bias.

Treatment arms designs can also be used to analyze the impacts of different intensities of a given intervention. As an example, teachers trainings could be conducted either once or twice a year. The marginal difference in outcome could inform the implementing agency about whether investing in a second yearly training is worth in terms of improvement of learning outcomes. The detailed information provided by treatments arms analysis can help answer manifold questions that are relevant to policy design and decision making. The embedment of treatment arms in impact evaluation can show whether the program components are substitutes or complements, or provide guidance in cost-effectiveness analysis.